칼만 필터(Kalman filter)의 이해-3편(Interacting multiple mode Kalman Filter)

 

 

이번에는 여러 시스템 모델을 사용해서 실행하는 Interacting multiple mode Kalman Filter(IMM Kalman Filter)에 대해서 알아보려고 한다.

Kalman Filter에대해서 공부하면 각각 시스템 모델마다 자연스럽게 한계를 느끼게 되고 여러 개를 동시에 사용하면 어떨까? 하는 생각을 하게됨.

 

그래서 나온 개념이 여러 모델을 사용해서 자동으로 합쳐주는 개념인 IMM Kalman Filter 임.

 

IMM Kalman Filter를 사용하면 여러 시스템 모델을 사용하므로 예외처리를 적게하면서 다양한 상황에 대해서 대응이 가능해짐.

 

그러나 만능은 아니고 잘 사용해야함. 대충 사용하면 1개 사용한거와 큰 차이 없음.

Interacting multiple mode Kalman Filter 정의 :

여러 시스템 모델(CV,CT,CA etc)을 사용해서 kalman filter를 사용하는 것임.

 

해당 글은 아래 사이트에 있는 코드와 글을 기반으로으로 작성되었음을 알립니다.

출처 : https://note.yongcong.wang/Self-Driving/Prediction/imm-for-prediction/

Interacting Multiple Models(IMM) for Prediction - Notebook

 

위 사이트에 자세히 잘 나와 있다. 그래도 수식이 많고 한 번에 이해하기 힘든데 칼만 필터 수식을 보고

 

앞뒤에 어떻게 수정되는지를 보면 이해하기 훨씬 쉽다.

 

선형 칼만 필터의 경우

 

추정 값 계산 :  $ X_k = A*X_{k-1} $

 

오차 공분산 계산 : $ P_k = A*P_{k-1}A^T + Q $

 

칼만 이득 계산 : $ K_k = P_k*H^T*(H*P_k*H^T + R)^{-1}$

 

추정 값 업데이트 : $ X'_k = X_k + K_k(z_k - H*X_k) $

 

오차 공분산 업데이트 : $ P'_k = P_k - K_k*H*P_k $

 

위와 같은 흐름을 가진다 여기서 추정 값 계산시 IMM은 모델이 여러개 이므로

 

$ X_{k-1} $ 이 여러개 모델의 입력 $ X^i_{k-1} $ 로 변경된다.

 

i 는 모델의 index를 나타낸다.

 

즉 2개의 모델을 사용하면 2개의 $ X^i_{k-1} $ 를 계산해야하고 3개의 모델을 사용하면 3개의 $ X^i_{k-1} $ 를 계산해야한다.

 

즉 각각 $ X^i_{k-1} $ 를 계산하기 위해서 각각 모델의 $ X^i_{k-1} $ 값을 가져다가

 

가중치와 transition matrix를 곱해서 평균을 내야 한다.

 

즉 모델은 2개 사용하면 i = 0,1값을 가질 것이고 모델을 3개 사용하면 i 는 0, 1, 2값을 가질 것이다.

 

여기서 중요한 개념이 나오는데 $ X^i_{k-1} $ 마다 차원이 다를것이므로 transition matrix가 필요하다는 것이다.

밑에적은 $ A^i $는 transition matrix를 의미함.

 

예로 모델 2개를 사용하고 1차원(X)으로 CV, CA인 경우

 

CV의 추정값 개수는 4개(X,Vx) 이고 CA의 추정값은(X,Vx,Ax) 이다.

 

이때 상태 방정식 차원이 CV 2개 CA는 3개임.

 

그래서 transition matrix는 아래 같은 구조를 가질 수 밖에 없다.

A = [ CVtoCV, CAtoCV          CVtoCA, CAtoCA ]

이렇게 되고 이것을 수식으로 나타내면

A[0][0] = [1 0

                0 1]

A[0][1] = [1 0 0

               0 1 0 ]

A[1][0] = [1 0

                0 1

                0 0]

A[1][1] = [1 0 0

                0 1 0

                0 0 1 ]

 

위 처럼 작성할 수 있다. 모델 A,B의 속성을 맞춰주는 adapter 같은 matrix이다.

 

$$ X^j_{k-1} = \sum_{i}^{r} A^i*X^i_{k-1}*u^i $$

 

i 는 모델 index를 말하고 r은 모델 개수를 말한다.

 

j 는 현재 모델 index를 의미한다.

 

위에 보면 각모델별 가중치를 자동으로 계산해주는 $u^i$ 가 있는데 the probability of model 을 의미한다.

코드를 보면 간단히 이해 할 수 있다.

u = np.dot(self.P_trans.T, self.U_prob)
mu = np.zeros(self.P_trans.shape)
for i in range(self.mode_cnt):
    for j in range(self.mode_cnt):
         mu[i, j] = self.P_trans[i, j] * self.U_prob[i, 0] / u[j, 0];

 

코드의 $ mu^i $ 가 수식의 $ u^i $ 를 의미한다.

 

약간 차원이 다른것은 수식 복잡하면 이해하기 어렵기 때문에 간단하게 적어서 그렇다.

for j in range(self.mode_cnt):
    for i in range(self.mode_cnt):
        X_mix[j] += np.dot(self.model_trans[j][i],
                            self.models[i].X) * mu[i, j]

P_mix = [np.zeros(model.P.shape) for model in self.models]
for j in range(self.mode_cnt):
    for i in range(self.mode_cnt):
        P = self.models[i].P + np.dot((self.models[i].X - X_mix[i]),
                                        (self.models[i].X - X_mix[i]).T)
        P_mix[j] += mu[i, j] * np.dot(np.dot(self.model_trans[j][i], P),
                                        self.model_trans[j][i].T)

 

$ X^i_{k-1} $ 가 위 코드 X_mix[j] 를 의미한다.

for j in range(self.mode_cnt):
    self.models[j].X = X_mix[j]
    self.models[j].P = P_mix[j]
    self.models[j].filt(Z)

 

그래서 위 처럼 각각 모듈마다 실행해서 업데이트 하면 됨.

 

$ P_j=\sum_{i}^{r} u_i * (P_i + X_i - X_{mix} )(P_i + X_i - X_{mix})^T $

for j in range(self.mode_cnt):
    mode = self.models[j]
    D = Z - np.dot(mode.H, mode.X_pre)
    S = np.dot(np.dot(mode.H, mode.P_pre), mode.H.T) + mode.R

    Lambda = (np.linalg.det(2 * math.pi * S)) ** (-0.5) * \
                np.exp(-0.5 * np.dot(np.dot(D.T, np.linalg.inv(S)), D))
    self.U_prob[j, 0] = Lambda * u[j, 0]
    self.U_prob = self.U_prob / np.sum(self.U_prob)

 

X 값 즉 상태 추정 값(estimated state)에대해서 업데이트 했으므로 오차 공분산 값에대해서도 업데이트 해야한다.

 

여기서 헷갈리면 안되는것은 kalman filter를 실행하기위한 각각 모델의 mixed 값이다.

 

$ u_i=p_i*U_i/\sum_{j}^{r} p_j*U_j $

 

여기서 p 는 the probability of model이고 U는 probability vector of each model 이다.

 

내가 볼때 IMM Kalman Filter는 Lamdda값 계산 이해가 핵심인데 이것을 설명하면

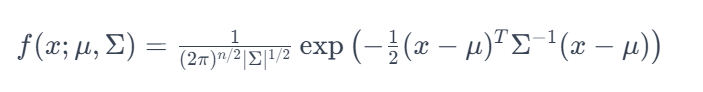
위는 가우시안 확률 밀도 함수이다. 변수 설명은 아래와 같다.

• x는 다변량 확률 변수
• μ는 평균 벡터입니다.
• Σ는 공분산 행렬입니다.
• ∣Σ∣는 공분산 행렬의 determinant입니다.
• n은 확률 변수의 차원, 즉 확률 변수의 개수 임

즉 Lamdda와 수식이 같은것을 볼수 있다.

 

다시 설명하면 평균과 어떤 값 x의 차이는 측정 값과 추정 값의 차이를 나타 냄.

 

그래서 측정 값과 예측 값의 차이를 가우시안 확률 분포로 확률을 계산함.

 

여기에 기존 모델 확률을 곱해서 최종 모델 확률을 곱하고 모델 확률 정규화를 통해서 확률 합이 1이 되도록 함.

 

즉 측정값에대해서 확률 밀도 함수를 통해서 확률을 계산 후

 

확률에따라서 weight를 설정하는것이다.

 

여기서 중요한것은 모델 확률 선택시 각 모델의 공분산 값을 사용하고 모델 선택 확률은 가우시안 확률 분포를 이용한다는 것이다.