칼만 필터 Kalmanfilter 의 이해-2편

 

이 편이 칼만필터의 시스템 모델에 대해서 설명할 것이다. 

 

사실 이 부분이 칼만 필터의 핵심이다.

 

즉 칼만필터를 이해하기 위해서는 시스템 모델을 이해해야한다.

 

그리고 측정 값과 시스템 모델의 관계도 이해해야 한다.

 

참고로 해당 글을 참조 했음을 알려둔다.

https://note.yongcong.wang/Self-Driving/Prediction/imm-for-prediction/

Interacting Multiple Models(IMM) for Prediction - Notebook

 

시스템 모델설계 방식과 측정 값과 시스템 모델의 관계에 따라서 선형 칼만 필터와 비선형 칼만 필터로 구분 된다.

 

두 부분이 다 선형이면 선형 칼만 필터이고

 

시스템 모델과 측정 값과 시스템 모델과의 관계 2개 중 하나가 선형이 아니면 비선형 칼만 필터가 된다.

 

비선형 칼만 필터를 푸는 방식에는 대표적으로 Extended Kalman Filter와 Uncented Kalman Filter가 있지만

 

난 Uncented Kalman Filter를 선호한다. 이유는 Jacobian 즉 편미분을 하지 않아도 되기 때문에

 

비선형 칼만 필터를 설계할때는 Uncented Kalman Filter를 선호함.

 

이제 시스템 모델에대해서 이해해보자

1. 선형 칼만 필터

일반적인 칼만 필터의 공식은 아래와 같은데 

 

추정 값 계산 :  $ X_k = A*X_{k-1} $

 

오차 공분산 계산 : $ P_k = A*P_{k-1}A^T + Q $

 

칼만 이득 계산 : $ K_k = P_k*H^T*(H*P_k*H^T + R)^{-1}$

 

추정 값 업데이트 : $ X'_k = X_k + K_k(z_k - H*X_k) $

 

오차 공분산 업데이트 : $ P'_k = P_k - K_k*H*P_k $

 

선형 vs 비선형 구분 기준?

A, H 을 상수로 구현할 수 있으면 시스템이 a + b + c 같은 선형 시스템이라는 의미므로 선형 칼만 필터이다. 

 

그러나 A, H matrix를 상수로 구현할 수 없으면 선형 시스템이 아니다.

 

자율 주행에서 CV((Constant Velocity)), CA((Constant Acceleration)), CT((Constant Turn rate)) 3개의 모델이 자주 사용되는데

 

판단 해보자!

 

측정 값은 x,y position 이라고 가정하면

CV((Constant Velocity)) model은 아래처럼 구현 할 수 있음. dt 는 상수이므로 모든 값이 상수이다. 그러므로 선형 칼만 필터이다.

시스템 변수	A	H
\begin{bmatrix}  X \\   V_x  \\  Y \\  V_y \\ \end{bmatrix}	\begin{bmatrix} 1&dt& 0& 0 \\ 0&1 & 0& 0 \\ 0&0 & 1& dt  \\ 0&0 & 0& 1 \\ \end{bmatrix}	\begin{bmatrix} 1 \\ 0 \\ 1 \\ 0 \\ \end{bmatrix}

 

즉 모든 행렬의 값이 상수로 구현되어 있는것을 알 수 있음.

 

그럼 다음으로 CA((Constant Acceleration))  model을 생각해보자!! 

밑의 A, H도 상수로 표현 되므로 밑의 시스템도 선형 칼만 필터로 구현 가능하다.

시스템 변수	A	H
\begin{bmatrix}  X \\  V_x \\  A_x \\  Y \\  V_y \\  A_y \\ \end{bmatrix}	\begin{bmatrix} 1& dt & 0.5*dt^2& 0 & 0 & 0 \\ 0& 1 & dt & 0 & 0 & 0 \\ 0& 0 & 1 & 0 & 0 & 0 \\ 0& 0 & 0 & 1 & dt & 0.5*dt^2 \\ 0& 0 & 0 & 0 & 1 & dt \\ 0& 0 & 0 & 0 & 0 & 1 \\ \end{bmatrix}	\begin{bmatrix} 1 \\ 0 \\ 0 \\ 1 \\ 0 \\ 0 \\ \end{bmatrix}

 

참고로 A는 state transition matrix 라고 부르고

H 는 observation matrix 라고 부른다. 

 

A는 시스템 모델을 의미하고 H는 측정값을 시스템 모델과 연결 시켜주는 역할을 하는 matrix다.

 

이제 마지막으로 CT((Constant Turn rate)) model을 보자

 

나도 이 모델을 다룰때 선형인지 비선형인지 헷갈렸다.

 

이유는 yaw rate을 어떻게 정의하느냐에 따라서 선형과 비선형 칼만 필터를 왔다 갔다 하기 때문이다. 

 

만일 차량의 yaw rate으로 매번 사용한다면 밑의 A matrix는 상수가 된다.

 

혹은 위에 링크된 예제에서는 고정된 값으로 사용하고 있어서 상수이므로 선형 칼만 필터로 설명하고 있다.

 

그러나 실제 타겟의 yaw rate값을 이용해서 구현 하고 싶다면 A matrix는 상수가 아니므로  선형 칼만 필터를 사용 할 수 없다.

 

그래서 실제 target의 yaw 를 사용하면 비선형 칼만 필터로 EKF 혹은 UKF를 사용해야한다. 

시스템 변수	A	H
\begin{bmatrix}  X \\  V_x \\  Y \\  V_y \\  \dot{\theta}(yaw\;rate) \\ \end{bmatrix}	\begin{bmatrix}  1 & \frac{sin(\dot{\theta} * dt)}{\dot{\theta}}& 0 & -\frac{1-cos(\dot{\theta} * dt)}{\dot{\theta}}& 0 \\ 0 & cos(\dot{\theta} * dt)& 0 & -sin(\dot{\theta} * dt)& 0 \\ 0 & \frac{1-cos(\dot{\theta} * dt)}{\dot{\theta}} & 1 & \frac{sin(\dot{\theta} * dt)}{\dot{\theta}}& 0 \\ 0 & sin(\dot{\theta} * dt)& 0 & cos(\dot{\theta} * dt)& 0 \\ 0 & 0 & 0 & 0 & 1 \end{bmatrix}	\begin{bmatrix} 1 \\ 0 \\ 1 \\ 0 \\ 0 \\ \end{bmatrix}

 

사실 비선형 칼만 필터를 사용할때는 위 처럼 시스템 모델을 가져가지 않는다.

 

CTRV 혹은 CTRA라고 하는데 

 

찾아보니 아래 논문이 잘 나왔있다. 

 

논문 제목 : Comparative evaluation of Kalman filters and motion models in vehicular state estimation and path prediction

링크 주소 :

https://www.researchgate.net/publication/352121423_Comparative_evaluation_of_Kalman_filters_and_motion_models_in_vehicular_state_estimation_and_path_prediction

 

논문에서 설명하는 시스템 모델 수식은 아래 처럼 잘 설명되어 있다.

 

논문에서는 EKF를 사용하고 있지만 내 생각에는 UKF가 더 좋을 것 같다.

 

 

 

그리고 마지막으로 그림이 좋아서 Udacity의 강의 자료인데 그림이 좋아서 가져와 봤다.

출처 : https://dsp.stackexchange.com/questions/43572/unscented-kalman-filter-equations-for-constant-turn-rate-and-velocity-process-mo

 

---

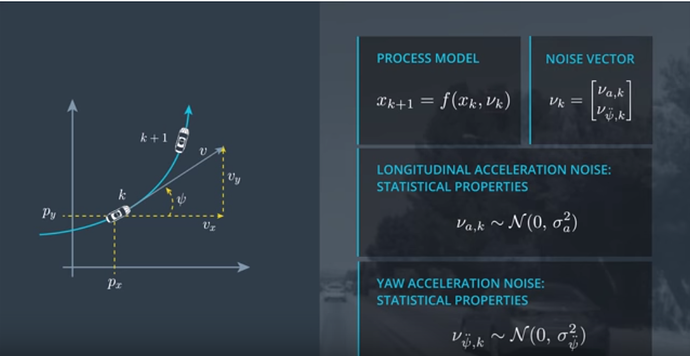
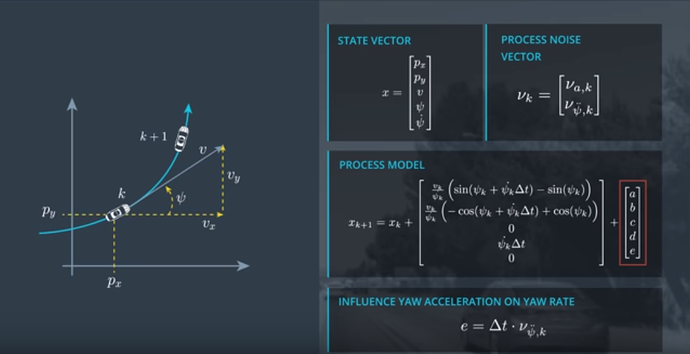
내가 볼때 비선형 칼만 필터 구현시 가장 중요한 Ucented Kalman Filter에 대해서는 시간될때 적어 보겠다.

 

사실 별거 없고 따라하면 된다. 단 어떻게 비선형 모델에서 공분산 값을 추출하는 지만 이해하면 된다.

 

다음 편은 내가 참조했던 사이트를 참조해서 IMM Kalman Filter에대해서 설명할 예정이다.